




When disaster strikes at the
Natural History Museum, can you and
your friends use math to escape?
START





















Congrats, you escaped the museum and saved the exhibits!
Would you like to play again?
RESTART
Did you know there are many careers that use math
to solve problems and make decisions?
Actuaries are experts who use math to:
Evaluate the likelihood of future events—using numbers, not crystal balls.
Design creative ways to reduce the likelihood of unwanted events.
Decrease the impact of unwanted events that do occur.
You, Anh, and Jeremiah have purchased three general tickets to the museum, plus three admissions to the special Giant Squid exhibit. The cost for all six tickets was $57. General museum tickets cost $5 more than the admission to the special exhibit. Which equation could you use to figure out how much each friend owes for the Giant Squid exhibit?
a3y + 3(x – 5) = 57 b3x + 3(x + 5) = 57 c6(x + x + 5) = 57 dDon’t know
Question 1 of 5



You, Anh, and Jeremiah have purchased three general tickets to the museum, plus three special admissions to the ecosphere exhibit. The cost for all six tickets was $63. Ecosphere admission costs $3 less than tickets to the museum. Which equation could you use to figure out how much each friend owes for their museum ticket?
a3x + 3y = 63 – 3 ÷ 3 b3x+ 3(x+3)=63 c3x + 3(x – 3) = 63 dDon’t know
Question 1 of 5



Jeremiah wants to see the Giant Squid exhibit on Floor -2 after you’ve finished Pterosaurs on Floor 3. Based on the Floor Directory to the right, which strategy and equation best describe the elevator ride you’d take from Pterosaurs to Giant Squid?
aWe should find the difference between Floor -2 and Floor 3.
-2 – 3 = -5
That means we’d take the elevator down 5 floors.
bWe should find the difference between Floor -2 and Floor 3.
-2 – 3 = |5|
That means we’d take the elevator up 5 floors.
cWe should find the sum of all floors.
-2 + -1 + 0 + 1 + 2 + 3 = 3
That means we’d take the elevator up 3 floors.
dDon’t know
Question 2 of 5




Jeremiah wants to see the Rooftop Rainforest on Floor 4 after you’ve finished Creatures of the Deep on Floor -3. Which strategy and equation best describe the elevator ride you’d take from Creatures of the Deep to the Rooftop?
aWe should count the floors, but skip the lobby since it’s equal to 0.
Floors: -2, -1, 1, 2, 3, 4
That means we’d take the elevator up 6 floors.
bWe should find the difference between Floor -3 and Floor 4.
4 – (-3) = 7
That means we’d take the elevator up 7 floors.
cWe should find the difference between Floor 4 and Floor -3.
-3 – 4 = -7
That means we’d take the elevator down 7 floors.
dDon’t know
Question 2 of 5




Anh wants to check out the nautilus fossil that’s close to 500 million years old! Use the exhibit labels and your knowledge of equivalent expressions to locate the display bookmarked on Anh’s phone.
Question 3 of 5



Anh wants to check out the nautilus fossil that’s close to 500 million years old! Use the exhibit labels and your knowledge of equivalent expressions to locate the display bookmarked on Anh’s phone.
Question 3 of 5



You are finishing up at the Meteorites exhibit. Next up, you want to head over to the Aquatic Mammals exhibit. How will you and your friends get there?
aFrom (-3, 1) we’ll head north to (3, 1), then travel west to (3, -7), covering a total distance of 18 units.
bFrom (1, -3) we’ll head north to (1, 3), then travel west to (-7, 3), covering a total distance of 14 units.
cFrom (-7, 3) we’ll head east to (1, 3), then travel
south to (1, -3), covering a total distance of 14 units.
dDon’t know
Question 4 of 5




Next up, you want to see the Giant Sequoia at the entrance of the Ancient Forests exhibit. How will you and your friends get there?
aFrom (0, -2) we’ll head South to (-3, -2), then travel East to (-3, 2), covering a total distance of 9 units. bFrom (2, -3) we’ll head West to (-2, -3), then travel North to (-2, 0), covering a total distance of 7 units. cFrom (-2, 0) we’ll head South to (-2, -3), then travel East to (2, -3), covering a total distance of 7 units. dDon’t know
Question 4 of 5




How confident are you about knowing which math skill to use to solve math problems?
aVery confident bConfident cSomewhat confident dNot confident
Question 5 of 5














































































































You, Anh, and Jeremiah found a tumbler online that you decide to buy
from the gift shop. Use the tags on the boxes and your knowledge of
equivalent expressions to pick the box off the shelf that matches the tumbler on the phone.
Question 1 of 5



You, Anh, and Jeremiah found a tumbler online that you decide to buy
from the gift shop. Use the tags on the boxes and your knowledge of
equivalent expressions to pick the box off the shelf that matches the tumbler on the phone.
Question 1 of 5



Thanks for visiting! Can you help other museumgoers plan their visit by answering some customer questions?
Customer Question: How much would it cost for my family of four to have snack packs at the cafe?
Pricing Info
• Four tickets to the museum plus four snack packs at the café cost $68
• Museum tickets cost $7 more than snack packs.
aSnack packs would cost $48 for a family of four.
I used the equation 4x + 4(x – 7) = 68 and proved that x is equal to 12. I multiplied my answer by 4 to find the cost for the whole family.
bSnack packs would cost $20 for a family of four.
I used the equation 4(x + 7) + 4x = 68 to find the cost of a snack pack. I multiplied my answer by 4 to find the cost for the whole family.
cSnack packs are $9.
I divided $72 by four people to get $18, then divided that in half to find the price of snack packs.
Question 2 of 5




Thanks for visiting! Help other museumgoers plan their visit.
Customer Question: I purchased 6 tickets to the museum plus a t-shirt at the gift shop for my grandson. I need to return the t-shirt because it doesn’t fit. How much is the refund?
Six museum tickets and a t-shirt cost $89. Museum tickets are $5 less than a t-shirt.
aYour refund would be $12.
I used x = the cost of a museum ticket and the equation 6x + x + 5 = 89 to find the answer.
bYour refund would be about $12.75.
I divided $89 by 7 (6 tickets and 1 t-shirt) to get the answer.
cYour refund would be $17.
I used x = the cost of a t-shirt and the equation x + 6(x – 5) = 89 to find the answer.
Question 2 of 5




Customer Question: Is the fourth floor’s rooftop Rainforest exhibit wheelchair accessible? How do you get there from the Giant Squid exhibit on floor -2?
aYes. The elevator goes all the way to the rooftop.
It’s 2 floors up from the Giant Squid, because 4 – 2 = 2.
bYes. You’ll need to ride the elevator from Floor -3 to Floor 4.
cYes. You can take the elevator straight up. It’s 6 floors up from the Giant Squid. I used 4 – (-2) = 6 to calculate
how many floors it is.
Question 3 of 5



Customer Question: How do you get from underground parking on floor -3 to the giant sequoia exhibit on floor 2?
aYou take the elevator up 5 floors.
I used 2 – (-3) = 5 to calculate the difference between the floors.
bYou take the elevator down 1 floor, because 2 + (-3) = -1.
cYou take the elevator down 5 floors.
I used -2 + (-3) = -5 to calculate the difference between the floors.
Question 3 of 5



Customer Question: How do you get to the café from the museum’s main entrance?
aYou need to head 8 units north from (1, -5) to (1, 3), then head east 6 units to the café entrance at (7, 3). bTravel from (-5, 1) to (3, 1). Turn east. You’ll see the café entrance at (3, 7). You’ll travel a total of 14 units. cTravel from (1, -5) to (1, -2). Travel east 6 units to (7, -2). The gift shop will be on your left.
Question 4 of 5




Customer Question: How do you get from the elevators to the parking garage?
aFrom (-4, -8) go east 3 units to (-4, -5). Turn right, then travel 4 units to (-8, -5).
The garage entrance is on your left.
bFrom (-5, -8) travel up 4 units to (-5, -4). Turn left and travel 3 more units to (-8, -4).
cThe elevators are on your right.
From (-8, -4) go east 3 units to (-5, -4). Make a right, then travel 4 units to (-5, -8). The garage entrance is on your left.
Question 4 of 5




How confident are you about knowing which math skill to use to solve math problems?
aVery confident bConfident cSomewhat confident dNot confident
Question 5 of 5




The femur fossil has tumbled to (-8, -9). We need to get it back into place at (1, 1). How many horizontal and vertical units do we need to move it? Listen to Anh and Jeremiah’s solutions to choose the best option.
Strategy! Let’s think of the problem like a triangle with these coordinates: (-8, -9) and (1, 1) and (1, -9). Click here to show the points.
Reasoning!
Let’s subtract to find the difference between the two x coordinates and the two y coordinates that make up each side. I’ll start with the bigger number and subtract the smaller one, since distance must be a positive number.
On the x-axis, 1 minus -8 means that the triangle’s base is 9 units long.
On the y-axis, 1 minus -9 means that the triangle’s height is 10 units, because subtracting a negative number is equivalent to adding a positive number.
Therefore! We need to move the femur 9 units right on the x-axis and 10 units up on the y-axis.
Choose a solution
Strategy! Let’s visualize the problem as a triangle with coordinates (-8, -9) and (1, 1) and (1, -9). Click here to show the points. Figuring out the triangle’s base and height will tell us the distances the Fossilifter needs to travel.
Reasoning!
Let’s subtract to find the difference between the coordinates on the x and y axes. I’ll go left to right on the coordinate plane, since equations are written left to right.
On the x-axis, -8 minus 1 is -7. Since this is a length indicating real space at the museum, I’ll use the absolute value of 7.
On the y-axis, -9 minus 1 is -8, or 8 in absolute value.
Therefore! If we reasoned correctly, we need to set the Fossilifter to move the femur 7 units right on the x-axis and 8 units up on the y-axis.
Choose a solution
The femur fossil has tumbled to (-8, -9). We need to get it back into place at (1, 1). How many horizontal and vertical units do we need to move it? Listen to Anh and Jeremiah’s solutions to choose the best option.
START
The fallen fossil has tumbled to (-3, -7). We need to get it back into place at (3, 1). How many horizontal and vertical units do we need to move it? Set the Fossilifter’s vertical and horizontal commands! Review Anh and Jeremiah’s reasoning and choose the correct solution.
Strategy! Let’s visualize the problem as a triangle with the coordinates (-3, 1) and (3, 1) and (-3, -7). Click here to show the points.
Reasoning! Let’s find the difference between the coordinates on the x- and y-axes using subtraction.
For the base, 3 minus -3 gives us a distance of 6 units.
For the height, 1 minus -7 is a distance of 8 units.
Therefore! I think we should set the Fossilifter to move the fossil 8 units right on the x-axis and 6 units up on the y-axis.
Choose a solution
Strategy! Let’s think of the problem like a triangle with coordinates (-3, -7) and (3, 1) and (3, -7). Click here to show the points.
Reasoning!
If we use subtraction, we can find the difference between the coordinates on each axis. In each equation, since distance must be a positive number, I’ll start with the bigger number and subtract the smaller one.
For the base, I see the two x coordinates are: -3 and 3.
I’ll start my equation with positive 3 because it’s the bigger number.
3 minus -3 means that the base is 6 units.
On the y-axis, 1 minus -7 means that the height is 8 units.
Therefore! I think that means we need to set the Fossilifter to move the fossil 6 units right on the x-axis and 8 units up on the y-axis.
Choose a solution
The fallen fossil has tumbled to (-3, -7). We need to get it back into place at (3, 1). How many horizontal and vertical units do we need to move it? Set the Fossilifter’s vertical and horizontal commands! Review Anh and Jeremiah’s reasoning and choose the correct solution.
START

In the earthquake, the museum lost power.
To restore power,
plug the wire into the
socket labeled with the
equivalent expression.
Listen to Anh and
Jeremiah’s reasoning and
choose the best solution.
Strategy! Let’s reorganize the expression -y + 7x + 14x -12y -15y by collecting like terms.
Reasoning!
First, I’m going to shuffle things around so I can put all of the x’s and y’s together.
I get 14x + 7x – 15y – 12y – y.
Then I’ll combine like terms by adding and subtracting, which results in 21x – 28y.
Therefore! I found that 21x – 28y is equivalent to -y + 7x + 14x – 12y – 15y.
Choose a solution
Strategy! Let’s collect like terms in the expression 7(3x – 3y + y).
Reasoning!
First, we’ll combine like terms within the parentheses by adding 3y and y.
Then, we’ll multiply each of the terms inside the parentheses by the 7 outside the parenthesis.
3x multiplied by 7 is 21x.
4y multiplied by 7 is 28y.
Therefore! We should plug the wire labeled 21x – 28y into 7(3x – 3y + y).
Choose a solution
In the earthquake, the museum lost power. To restore power, plug the wire into the socket labeled with the equivalent expression. Review Anh and Jeremiah’s reasoning and choose the best solution.
START


In the earthquake, the museum lost power.
To restore power,
plug the wire into the
socket labeled with the
equivalent expression.
Listen to Anh and
Jeremiah’s reasoning and
choose the best solution.
Strategy! Let’s use the distributive property on the socket labeled
3(2x +3y).
Reasoning!
First, multiply 2x by 3 to get 6x.
Then, multiply 3y by 3 to get 9y.
Therefore! I think we should plug 6x + 9y into 3(2x +3y) because they’re equivalent expressions.
Choose a solution
Strategy! I’ll expand the expression 6(x + 3y).
Reasoning!
First, I’ll add 6 and x to get 6x.
Then, I’ll add 6 and 3y to get 9y.
Therefore! If I did the addition correctly, we should plug 6x + 9y into
6(x + 3y) because they’re equivalent expressions.
Choose a solution
In the earthquake, the museum lost power. To restore power, plug the wire into the socket labeled with the equivalent expression. Review Anh and Jeremiah’s reasoning and choose the best solution.
START
Jeremiah has tried all of the silver and gold keys on the key ring without any luck. By process of elimination, that means the key that unlocks the service elevator must be a brass key! What is the maximum number of keys Jeremiah might need to try in the lock? Review Anh and Jeremiah’s reasoning and choose the correct solution.
Strategy! Let’s write an algebraic expression and use k to stand in for the number of keys we need to try in the lock.
Reasoning!
First, we’ll establish that there are 48 keys in total.
On the right side of the equation, we’ll represent the silver and gold keys (3 times silver and 4 times gold). That’s 48 = (3 x 4) x k.
Then we’ll multiply everything in the parentheses by the variable k (since silver and gold keys are 3 times and 4 times the unknown variable).
If we combine like terms, we end up with 48 equals 12k.
After we use division to isolate the variable k, we get 4.
Therefore! We’ll be able to unlock the elevator if we try, at most, 4 brass keys.
Choose a solution
Strategy! Let’s set up an algebraic equation.
Reasoning!
First, we’ll establish that b stands for the number of brass keys.
Then we’ll write an equation: Silver keys plus gold keys is equal to the total number of keys on the ring minus the brass keys. That’s 3b + 4b = 48 - b.
If we use addition to combine like terms, we end up with 8b equals 48.
After we use division to isolate the variable b, we get 6.
Therefore! We can unlock the elevator if we try up to 6 brass keys.
Choose a solution
Jeremiah has tried all of the silver and gold keys on the key ring without any luck. By process of elimination, that means the key that unlocks the service elevator must be a brass key! What is the maximum number of keys Jeremiah might need to try in the lock? Review Anh and Jeremiah’s reasoning and choose the correct solution.
START
You’ve found another set of keys. Anh has tried all of the brass and silver keys without any luck. That means the key that unlocks the service elevator must be a gold key! How many more keys does your group need to try in the lock? Listen to Anh and Jeremiah’s solutions to choose the best option.
Strategy! Let’s write an algebraic equation and use g to stand in for the number of keys we need to try in the lock.
Reasoning!
Let’s set up parentheses to represent the silver and brass keys (5 times and 4 times).
We’ll make the right side of the equation equal to 40—the total number of keys on the ring.
That’s (5 x 4) x g = 40.
Next we’ll multiply everything in the parentheses by the variable g (since silver keys are 5 times the unknown variable and brass keys are 4 times the unknown variable). That’s 5g x 4g = 40.
Finally, we’ll multiply the g terms together to get 20g. When we solve for g we get 2.
Therefore! We should be able to unlock the elevator if we try 2 gold keys.
Choose a solution
Strategy! We should think of the number of gold keys like an unknown variable.
Reasoning! If we subtract the number of silver keys and the number of brass keys from the total number of keys, we’ll be left with the number of gold keys! Let’s set up an equation.
I’ll start the equation with the number of keys, 40.
I’ll have k represent the number of gold keys.
Silver is 5k (5 times gold keys) and brass is 4k (4 times gold keys).
That’s 40 – 5k – 4k = k.
If we combine like terms, we end up with 40 equals 10k.
After we use division to isolate the variable k, we get 4.
Therefore! If we set up the equation correctly, we need to try 4 gold keys in the elevator!
Choose a solution
You’ve found another set of keys. Anh has tried all of the brass and silver keys without any luck. That means the key that unlocks the service elevator must be a gold key! How many more keys does your group need to try in the lock? Listen to Anh and Jeremiah’s solutions to choose the best option.
START

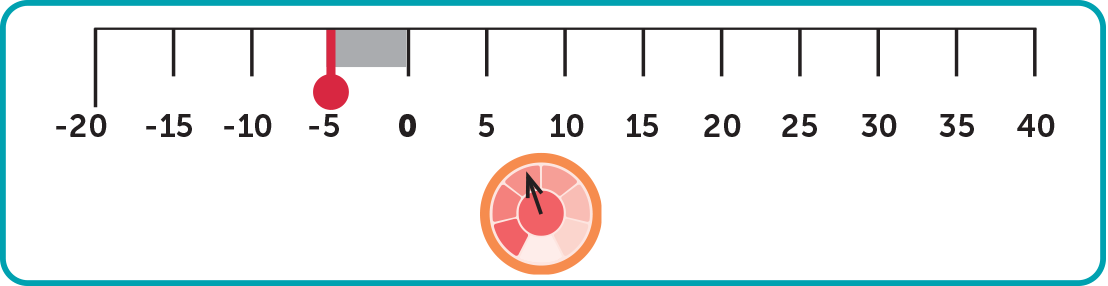

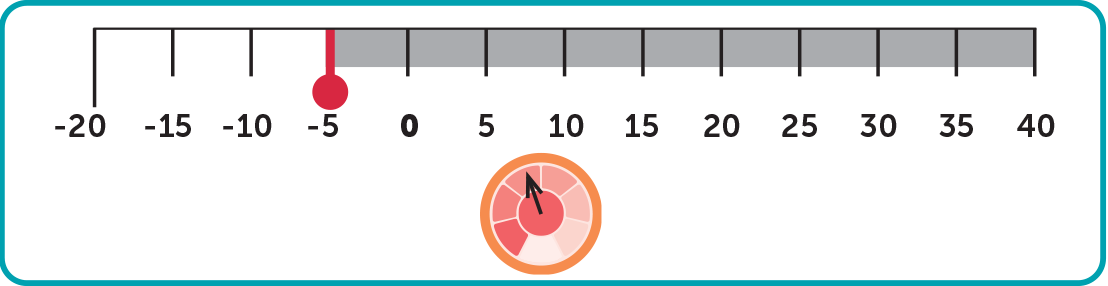

The temperature inside the insect display is –5 °F. It should be set to 40°F.
How many degrees should you and your friends turn the knob in order to return to the correct temperature? Review Anh and Jeremiah’s reasoning and choose the correct solution.
Strategy! Let’s think of the temperature control like a number line.
Reasoning!
On the negative side of the number line, the difference between -5 and 0 is -5, or 5° in absolute value.
On the positive side, the difference between 0 and 40 is 40°.
If we add 5° and 40° together, we get a total of 45°.
Therefore! I think we need to turn the temperature control knob up by 45°.
Choose a solution
Strategy! Let’s find the difference between the temperatures using subtraction.
Reasoning! If we take 40° and subtract negative 5°, we get 35°.
Therefore! We need to turn the temperature up by 35°.
Choose a solution
The temperature inside the insect display is -5 °F. It should be set to 40°F.
How many degrees should you and your friends turn the knob in order to return to the correct temperature? Review Anh and Jeremiah’s reasoning and choose the correct solution.
START

The butterfly display case is also fogging up! The temperature inside the display is 70 °F. It should be set to
-10 °F. By how many degrees does the temperature need to be adjusted? Review Anh and Jeremiah’s reasoning and choose the correct solution.
Strategy! Let’s use subtraction to find the difference between the two temperatures.
Reasoning!
To get from 70° to -10°, I need to use subtraction, 70° – (-10°). That gives me two negative signs in a row.
Subtracting a negative number is the same as adding a positive.
So 70° – (-10°) becomes 70° + 10°, which is 80°.
Therefore!
We need to turn the temperature down by 80°.
Choose a solution
Strategy! Let’s use addition to move from one temperature to another.
Reasoning!
I’ll combine the current temperature of 70° with the goal temperature of -10°, which will tell me how much to move the control dial.
70° plus -10° is 60°.
Therefore!
We should turn down the temperature by 60°.
Choose a solution
The butterfly display case is also fogging up! The temperature inside the display is 70 °F. It should be set to -10 °F. By how many degrees does the temperature need to be adjusted? Review Anh and Jeremiah’s reasoning and choose the correct solution.
START