Geometry Lesson Plan: Finding Missing Angle Measures

In this lesson, students will use supplementary, complementary, adjacent, and vertical angles to find missing measurements.

Preinstructional Planning

Objectives

 Students will:

• Define the angle-related terms supplementary, complementary, adjacent, and vertical
• Find missing angle measurements using their knowledge of these angle-related terms 
• Write and solve equations to find missing angle measurements

Materials

• What’s Your Angle? Finding Missing Angle Measurements printable
• Answer Key: Designing With Geometry printable
• Standards Chart: Geometry printable
• Optional: What’s the Angle? Bonus Worksheet printable

During Instruction

Set Up

1. Make a class set of the What’s Your Angle? Finding Missing Angle Measurements printable.

2. Print a copy of the Answer Key: Designing With Geometry printable for your use.

3. Optional: Make a class set of the What’s the Angle? Bonus Worksheet printable.

Lesson Directions

Introduction to Finding Missing Angle Measurements 

Step 1: Draw right angle ABC on the board. Ask how a math problem might indicate that the angle is a right angle. Students should be familiar with all of the following:

• The problem indicates the angle is a right angle or a 90º angle
• The problem indicates that one line is perpendicular to the other
• The square notation is used at the vertex
• The problem indicates that the angle is part of a rectangle, right triangle, etc.

Step 2: Create two complementary angles by adding ∠ABD inside the right angle. Indicate that ∠ABD = 50º. How can we find the measurement of ∠DBC? Tell the class that if ∠ABC is a 90º angle, then ∠ABD + ∠DBC must also equal 90º. x (the unknown angle) + 50º = 90º, so x = 40º.

Note that when two angles add up to 90º, they are called complementary. One way to remember the term is that complementary angles add up to 90º, and 90º angles form at corners. Also note that complementary angles don't have to be adjacent (next to each other); they just have to add up to 90º.

Step 3: Draw lines AC and DE that intersect at point B. Two sets of adjacent supplementary angles are created. For example, ∠ABE and ∠EBC are adjacent because they are next to each other and supplementary because their measurements add up to 180º. We know they add up to 180º because they each include sides that are part of the line AC and there are 180º in a line.

To remember the term supplementary angle, think of straight line. Mention that, just as with complementary angles, supplementary angles don't have to be adjacent; they just have to add up to 180º.

Step 4: Demonstrate how we can use our knowledge of supplementary angles to find missing angle measurements. Indicate that ∠ABE = 135º and we want to find the measurement of ∠EBC. If ∠ABE + ∠EBC = 180º, then 135º + x = 180º (where x represents ∠EBC) and we can calculate that ∠EBC = 45º.

Step 5: Note that when angles are formed when lines intersect, the angles opposite each other, called vertical angles, have equal angle measurements. Using the same drawing, demonstrate that ∠ABE = ∠DBC and ∠ABD = ∠EBC. If ∠ABE + ∠EBC = 180º and ∠DBC+ ∠EBC = 180º, then ∠ABE = ∠DBC. If necessary, repeat the process to show that ∠ABD = ∠EBC.

Step 6: Using the same drawing, add line segment BF, which creates angles ABF and FBE from angle ABE. Indicate that ∠ABF = 58º and ∠ABD = 72º. What is the measurement of ∠EBF? First, if ∠ABD = 72º then ∠ABE= 108º. If ∠ABE = 108º, and ∠ABF + ∠FBE = 108º, then ∠FBE must = 50º (108º - 58º = 50º).

There are other paths to this solution, and, if necessary, demonstrate how the answer could be obtained using other angles in the drawing (or have student volunteers explain).

Guided Practice

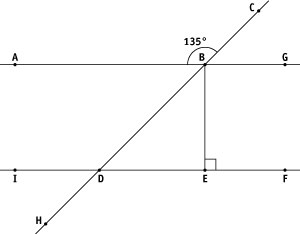
Step 7: Draw the illustration above on the board or provide students with a copy. Indicate that ∠ABC = 135º. Ask the class to pair up and find the measurement of ∠ABD, ∠CBG, and ∠GBE.

Answers: 

• ∠ABD = 45º because it and ∠ABC are supplementary. 180º - 135º = 45º.
  ∠CBG is also 45º because it and ∠ABD are vertical angles. 
• ∠GBE = 90º, proven with the following steps: If ∠ABD = 45º, then ∠DBE must also equal 45º because the two angles are complementary. ∠CBG + ∠DBE + ∠GBE must add up to 180º because they all "fit" on a straight line. So, 180º - (45º + 45º) = 90º.

Step 8: Checking for Understanding: Review answers as a class and respond to any questions.

Independent Practice

Step 9: Assign the What’s Your Angle? Finding Missing Angle Measurements printable for classwork or homework.

Step 10: Checking for Understanding: Review the answers to the What's Your Angle? Finding Missing Angle Measurements printable, which are provided on page 1 of the Answer Key: Designing With Geometry printable. Make sure students explain their mathematical thinking. Address any misconceptions that may arise.

Lesson Extension

Assign the What’s the Angle? Bonus Worksheet printable for classwork or homework.

Post Instructional

Standards

Grade 7: Finding Missing Angle Measurements (CCSS 7.G.B.5)

Grades 6–8: Making Sense of Problems, Reasoning, Constructing an Argument, Attending to Precision, Using Structure, Looking for Repeated Reasoning (CCSSMP1–3 and 6–8); NCTM Geometry

For more information, download the comprehensive Standards Chart: Geometry printable.